МЕЖДУНАРОДНИ ОЛИМПИАДИ ПО МАТЕМАТИКА 1959-1978

Началото

Идеята за провеждане на международни олимпиади по математика (МОМ) възниква на IV конгрес на румънските математици през 1956 година. Целта е да се постави началото на научно сътрудничество между млади и талантливи математици и така да се подпомогне изграждането на новото поколение изследователи в областта на математиката. Международните олимпиади по математика дават възможност за личен контакт между участниците – ученици и ръководители, за размяна на мнения относно преподаването на математиката в училищата и неговото развитие, за съревно­вание между млади математици от различни страни, за изводи относно тяхната подготовка.

Първите 20 международни олимпиади по математика МОМ I-XX се провеждат в периода 1959-1978 г. Те оказват силно влияние върху развитието на математическото образование в България – вж тук.[su_row][su_column size=”1/2″]

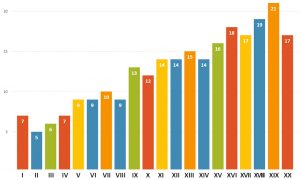
[/su_column][su_column size=”1/2″]Първата международна олимпиада по математика (МОМ I) се про­вежда през 1959 година в Румъния. В нея вземат участие седем европейски страни (само от социалистическия лагер), между които и България. Постепенно в МОМ I-XX (1959-1978) се включват страни от различни части на света (общо 24):
Австрия, Алжир, Англия, Белгия, България, Виетнам, ГДР (Германска демократична република), Гърция, Италия, Куба, Монголия, Полша, Румъния, САЩ, СССР (Съюз на съветските социалистически републики), Турция, Унгария, Финландия, Франция, ФРГ (Федерална република Германия), Холандия, Чехия, Швеция, Югославия. [/su_column][/su_row]

Организация на [su_tooltip style=”light” position=”north” rounded=”yes” content=”Международна олимпиада по математика”]МОМ[/su_tooltip]

На първата международна математическа олимпиада в Румъния (1959) се определят правилата за участие и общата организация на [su_tooltip style=”light” position=”north” rounded=”yes” content=”Международната олимпиада по математика”]МОМ[/su_tooltip]. Вземат се решения относно провеждането на олимпиадите, числеността на отборите, подборът на конкурсните задачи, оценяването, наградите, журирането.

Провеждане. Олимпиадите се провеждат всяка година през м. юли в някоя от страните участнички, в два състезателни дни, като всеки е с продължителност четири часа и с три задачи.

Отбори. Всяка страна има право да участвува с отбор най-много от осем ученици до двадесетгодишна възраст, които определя чрез вътрешна олимпиада или по друг начин. Всеки отбор трябва да има научен и педагогически ръководители. В частност, българският отбор се подбира измежду участниците с най-добри резултати в Националната олимпиада (вж Българското участие).

Международно жури. Олимпиадата се ръководи от Международно жури, съставено от научните ръководители на страните участнички и председател от страна на домакините. Решенията се вземат с явно гласуване. При равен брой гласове се приема мнението на групата, в която е председателят на журито.

Подбор на конкурсните задачи. Всяка страна изпраща от три до пет задачи, които се разглеждат от страната домакин и след предварителен подбор се пред­ставят пред международното жури. То избира шест задачи (по три за всеки състезателен ден), определя броя на точките за всяка от тях и уточнява изискванията към решенията на отделните задачи. Ръководителите на всеки отбор превеждат избраните задачи на съот­ветния език.

Класиране, награди. Преглеждането и оценяването на задачите се извършва от ръководителите на отборите. Страната домакин определя свои математици за координатори, кои­то също преглеждат решенията на задачите на всички участници в състезанието и уеднаквяват оценките. При координирането на оценките на учениците от страна­та домакин участвуват и ръководителите на отбори от страните, от които са включените в състезанието задачи. Окончателните оценки се уточняват на разширено съве­щание на международното жури, на което присъствуват и координаторите.

Класирането е индивидуално. На всяка олимпиада международното жури определя критериите и минималния брой точки, за които се присъждат I-ва, II-ра и III-та награди. Съотношението между трите награди е приблизително 1 : 3 : 5. В зависимост от резултатите, журито има право да присъжда и специални награди (например за оригинално решение), да дава грамоти и материални награди.

Закриване на олимпиадата

Всяка олимпиада завършва с тържествен акт, на който освен участниците, ръководителите и организаторите, присъстват преподаватели по математика, обществени дейци и др. Отчитат се резултатите и се връчват наградите на учениците. Поднасят се поздравления. Определя се страната-домакин на следващата олимпиада.

Източници

1. Будуров, Стоян. Математически олимпиади. – София : Народна просвета, 1972, 533 с.
2. Кендеров, П., Д. Серафимов, П. Димитрова. Международни олимпиади по математика. – София : Народна просвета, 1981, 224 с.

(Съставил: Р. Калтинска)

начало